Fomos ensinados que as raízes reais de uma equação quadrática correspondem aos locais onde o gráfico da função cruza o eixo das abcissas. Mas o que acontece quando a equação só tem raízes complexas? É possível encontrar uma interpretação geométrica também?
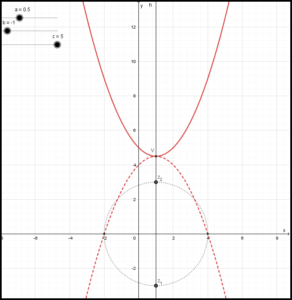
Há uma construção geométrica muito conhecida que localiza as raízes complexas de uma parábola usando um linha vertical que passa pelo vértice e intersecta um círculo com diâmetro dado pelos pontos de intersecção da parábola refletida com o eixo x. O seguinte applet ilustra essa construção passo a passo.
E por que funciona?
A equação da parábola refletida é ![]() .
.
Usando a fórmula clássica para resolução das equações quadráticas, é fácil mostrar que as raízes dessa parábola refletida, rotacionadas 90º no sentido anti-horário (em relação ao ponto médio), são iguais às raízes da parábola original, quando interpretadas como pontos do plano complexo.
só deixando meu gostei