A multiplicação e a divisão podem ser executadas mais facilmente quando utilizamos a forma polar (trigonométrica) de representação.
Esse applet, além de mostrar como essas operações são executadas na forma trigonométrica, fornece uma interpretação geométrica para elas.
Como usar este applet:
1 – Selecione a operação desejada (multiplicação ou divisão).
2 – Ao escolher a divisão, é possível decidir se deseja visualizar também o inverso multiplicativo de 
. Você pode pensar na divisão por como sendo a multiplicação de 
pelo inverso multiplicativo de .
3 – Informe os valores de e ou arraste-os no plano complexo até a posição desejada.
4 – Observe o resultado e a interpretação geométrica associada a esse resultado.
Exploração:
A multiplicação de números complexos 
pode ser interpretada geometricamente como uma homotetia (dilatação ou contração) de razão 
e uma rotação por um ângulo 
aplicadas ao vetor 
que representa . Assim, o número complexo 
tem módulo 
e argumento 
.
- Escolha os valores para 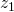e 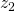de tal modo que eles sejam reais. O que acontece nesse caso? Os resultados são semelhantes àqueles obtidos com a multiplicação e divisão no conjunto dos números reais?
- Escolha valores para 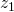e 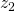de tal modo que eles sejam imaginários puros.
- Explore a multiplicação de um número complexo qualquer pela unidade imaginária i e a rotação associada a essa operação.
- Escolha 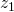com módulo unitário e verifique que, nesse caso, apenas a rotação é observada, uma vez que o módulo do produto não se altera.
- Escolha valores de tal forma que
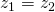. Tente estabelecer como seria o produto de 
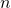números complexos iguais, isto é, 
.
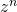Observação: A fórmula para se obter para z^n, conhecida como Fórmula de De Moivre, é:
![z^n = r^n [cos(n\theta) +i\, sen(n\theta)]](https://complexos.blog.br/wp-content/ql-cache/quicklatex.com-466aa24a6e4438ff8f68b7e6c83749d0_l3.png "Rendered by QuickLaTeX.com")