O Teorema Fundamental da Álgebra (TFA) afirma que todo polinômio com grau maior ou igual a 1 e coeficientes complexos tem uma raiz complexa.
Existem muitas demonstrações desse importante teorema. Gauss, por exemplo, o demonstrou de 4 modos diferentes durante a sua vida.
Essas demonstrações requerem uma série de conhecimentos matemáticos que não são vistos no Ensino Médio.
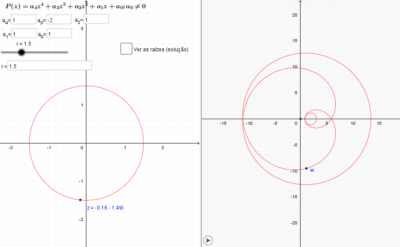
O seguinte applet apresenta uma forma de visualizar uma conhecida prova topológica do TFA, utilizando um polinômio de grau 4. O raciocínio utilizado pode ser estendido para polinômios de outros graus.
Mesmo que os alunos do Ensino Médio não conheçam os detalhes topológicos necessários para compreender por que a curva necessariamente passa pela origem quando variamos r, esse applet reforça a validade do TFA ao menos de forma visual.
Como funciona este applet:
A janela da esquerda mostra um círculo c com centro na origem do plano complexo e raio r. O número complexo z está posicionado nesse círculo e pode assumir qualquer valor à medida que variarmos r e o rotacionemos sobre o círculo c.
A janela da direita mostra uma curva fechada que é a imagem do polinômio P em c. Para r suficientemente pequeno, todo elemento de P(c) estará perto de 
e a origem do plano complexo estará no exterior da curva P(c). Para r suficientemente grande, a curva P(c) se assemelhará a n círculos do plano complexo centrados em e a origem do plano complexo estará no interior da curva P(c).
Assim, temos que a origem passa do interior para o exterior da curva à medida que variamos r. Aceitando-se que essa variação de r se dá de forma contínua, então, necessariamente, existe algum valor de z para o qual o polinômio P(c) passa sobre a origem, isto é, existe um valor de z tal P(z) = 0. Este valor de z é uma raiz de P, como previsto no TFA.
Como usar esse applet:
- Na janela da esquerda varie o valor de r até que a curva da janela da esquerda passe sobre a origem. Use o zoom das duas janelas para garantir um bom posicionamento sobre a origem.
- Quando a curva P(c) estiver posicionada sobre a origem na janela da esquerda, desloque o número complexo z até que sua imagem (w) atinja a origem (w = 0 + 0i). Quando isso acontecer, o valor de z é uma das raízes. Lembre-se de deslocar z completamente sobre o círculo c, pois pode haver mais de uma raiz.
- Repita o procedimento, isto é, varie r , encontre outros pontos em que P(c) passa sobre a origem e encontre as outras raízes.
O que mais você pode fazer com esse applet:
- Você pode modificar os coeficientes do polinômio P e repetir todo o processo. Esse applet permite polinômios de 1º, 2º, 3º e 4º graus. Lembre-se de escolher o valor dos coeficientes de modo que a curva P(c) caiba dentro da janela sem necessidade de ficar aplicando muito zoom.
- Você pode animar o deslocamento do ponto z sobre o círculo c e ver como ponto w (imagem de z) se desloca sobre P(c).
- Depois de localizar as raízes de P(z) manualmente, você pode conferir o resultado exibindo a solução.
Alguns valores para testar esse applet:
Esse applet do Geogebra se baseia no artigo Ilustración de una demostración del Teorema Fundamental del Algebra do professor Marcos Kiwi da Universidade do Chile.