Dizer que a Identidade de Euler é a equação mais bela da Matemática pode ser um tanto controverso. No entanto, não são poucos os cientistas que têm essa opinião. Veja, por exemplo, este artigo da revista Physics World que descreve um experimento psicológico que monitorou com ressonância magnética o cérebro de 15 cientistas ao visualizarem equações matemáticas. Ou ainda, esta pesquisa da BBC conduzida entre matemáticos e físicos em 2016.
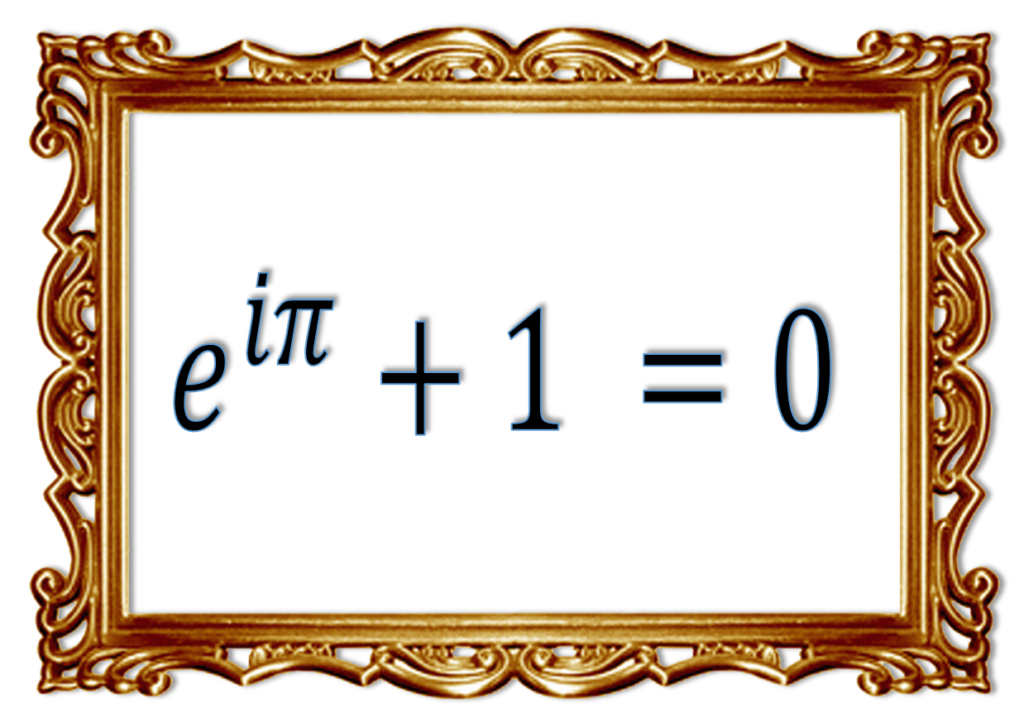
Esse fascínio provocado pela Identidade de Euler, provavelmente, vem do fato que ela reúne em uma só equação 5 das mais fundamentais constantes da Matemática (
e três operações aritméticas básicas (adição, multiplicação e potenciação).
A Identidade de Euler é, na verdade, apenas um caso particular da Fórmula de Euler, sendo obtida quando 
.
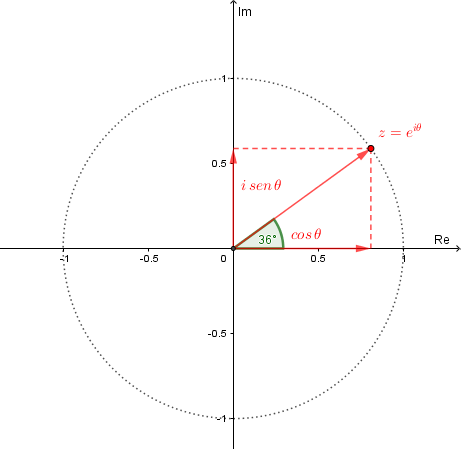
O seguinte applet permite visualizar a Fórmula de Euler no plano complexo e, portanto, também nos mostra a Identidade de Euler. Explore esse applet e veja como é possível obter a Identidade de Euler nele. Além disso, observe que, a partir da Fórmula de Euler, podemos representar qualquer número complexo na forma exponencial 
.
Como utilizar esse applet:
1 – Clique o botão Play para iniciar a animação e veja os diversos valores assumidos por z à medida que ele percorre o círculo unitário centrado na origem do plano complexo.
2 – Clique em <Parar na Identidade de Euler> para parar a animação pare quando e observe a obtenção da Identidade de Euler.
3 – Desmarque <Parar na Identidade de Euler> para continuar a animação.
Exploração:
1 – O que acontece quando 
? Use esse resultado para mostrar que 
é um número real. Usando uma calculadora, calcule o valor encontrado para .
2 – O valor obtido no item anterior é único? O que acontece quando 
? Usando a calculadora, forneça outro valor para .